非對稱加密？到底是什麼鎖可以有兩把鑰匙，用簡單數學解釋給你聽

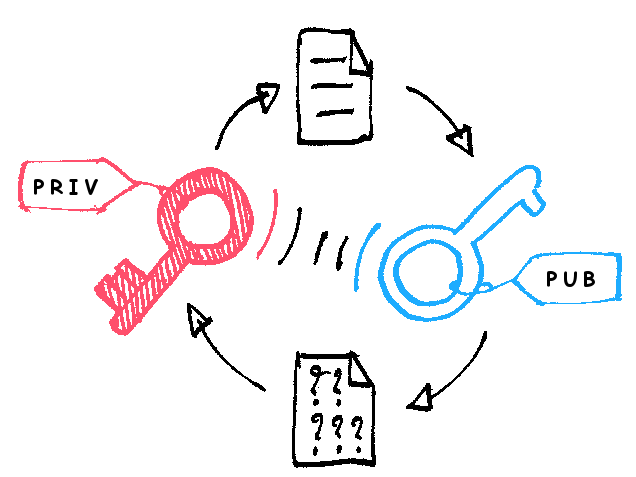
常聽到非對稱加密是用兩把鑰匙來做，但兩把鑰匙可以用一把來加密一把來解密，到底是什麼鎖可以做到這件事情？這篇文用簡單數學來告訴你這什麼邏輯。

非對稱加密用在很多地方，像是 HTTPS 協定、區塊鏈、免密碼登入 SSH等等。原則上你準備一組公私鑰，把公鑰給別人、私鑰留給自己，這樣就可以證明訊息是由你發出去的。

我們先舉個例子好了，我手上有一把私鑰是 91、公鑰是 11。我請你想一個三位數，把這個三位數和公鑰相乘，但只告訴我最後三位數就好，透過私鑰我就可以知道你想的三位數是多少。比方說你腦袋裡想著三位數（原文） 123，你乘以 11（公鑰）得到乘積 1,353 後，給我後面三位數，也就是 353（密文），我得到 353（密文）後再乘以 91（私鑰），最後得到的 32,123，後面三位數就是你心目中原本想的三位數 123（原文）了。

整理一下：

• 私鑰：91
• 公鑰：11
• 密文：353
• 原文：123

這原理其實很簡單，因為 91 × 11 是 1001，任何數乘上 1001，末三位數都不變。知道原理以後就知道，只要兩個質數乘起來是 X00...001，我就可以拿來做這個運算。

再舉一個例子──現在我算好一個私鑰了，我先不告訴你。而我將原文乘以私鑰後，取後八位數告訴你是：56,770,078，我只告訴你公鑰是 20201，你可以用 20201 乘以 56,770,078 取後八位得到原文是 12345678。

整理一下：

• 私鑰：（我沒有告訴你）
• 公鑰：20201
• 密文：56770078
• 原文：12345678

你覺得你能算出私鑰是多少嗎？

這題的答案到文末再公布，不過我要再舉一個例子。如果你覺得只能取八位數太少的話，那你用 1199481995446957 × 3334772856269093 = 4000000000000000000000000000001，就有了一個可以存 30 位數的非對稱加密系統。

不過，在實際場域，非對稱加密演算法（如 RSA）不會用乘積那麼簡單的例子，而是用指數和模除的方式來運算。如果想知道 RSA 具體怎麼算的，可以看看 這篇 文章。

雖然公鑰丟出來、密文也丟出來，我就可以解開原文了，但有時候公私鑰加密是拿來驗證你是不是本人。例如你把私鑰留著，公鑰給我，我今天要測試你是不是本人，我可以丟一段測試訊息（assertion）給你，你用私鑰來加密這個訊息（signature），我用公鑰來解開看你的簽名是不是符合我原本的 assertion。

之後會再來舉一些實務上簽名的應用。

最後，上面那題的私鑰是 19801。驗算一下：

$12345678 \times 19801 = 244456770078$
$56770078 \times 20201 = 1146812345678$

參考資料

• Asymmetric encryption algorithm RSA learning